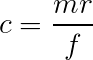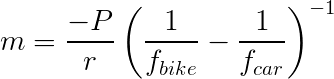For performing elemental analysis by x-ray photoelectron spectroscopy, I needed to integrate and find the area under the peaks in some spectra. One approach is to fit each peak with a Gaussian function and use the area of the Gaussian. For some convoluted peaks, I wanted something simpler. I wanted to get the total area under each peak without fitting it in any way.

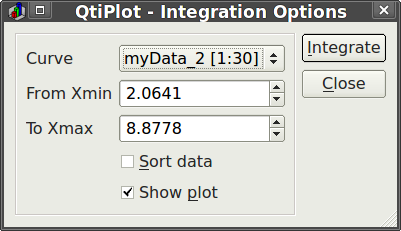
I use QtiPlot almost exclusively for plotting and fitting (fityk is my other go-to program) and one of the menu options for plots is Analysis->Integrate. That option brings up a tiny dialog where you can select the curve and range over which to integrate.

In the results log, an area is printed for the integrated curve. I wasn’t sure what QtiPlot was doing so I did an experiment with a simple set of data. I now know conclusively the algorithm used by QtiPlot and am able to replicate it in a spreadsheet program. I use LibreOffice Calc, but the instructions here should work in Excel as well.

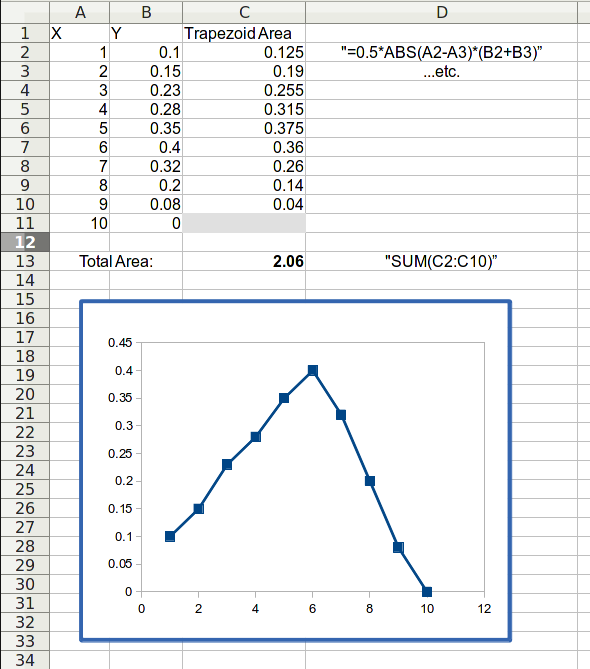
Given a set of n points, P₁ through P_n, a curve is generated by connecting each point with straight lines.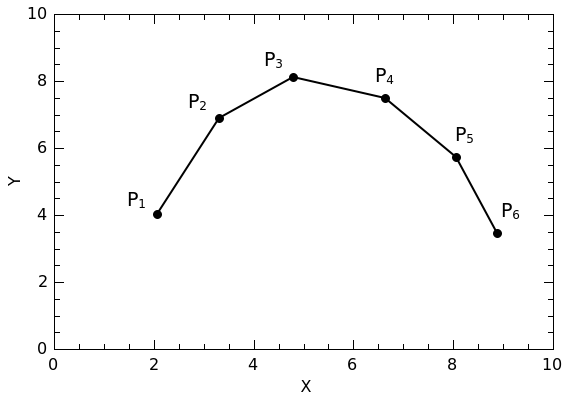

The area under the curve between two points, (x₁, y₁) and (x₂, y₂), is a trapezoid with area A = 1/2 |x₁ – x₂| (y₁ + y₂).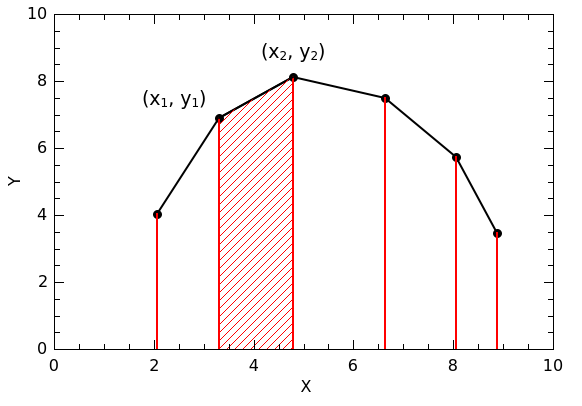

To find the area under the curve defined by a set of points, QtiPlot iterates through the points from P₀ to P_n-1. For each point P_i, it calculates the area using P_i as (x₁, y₁) and P_i+1 as (x₂, y₂) and sums all of the trapezoid areas.

The above process is easy to replicate in LibreOffice Calc (or Excel) with the x,y data that define the curve. Assuming the x coordinates are in column A starting at row 1 and the y coordinates are in column B starting row 1, the areas of the individual trapezoids can be generated in column C. The formula in the first row is: “=0.5*abs(A1-A2)*(B1+B2)”. That formula is then copied down column C in all of the rows but the last. Finally, the areas are summed to give the total area under the curve.

In deciding whether or not purchasing a motorcycle is a prudent decision, cost plays a significant factor. Motorcycles often get much higher gas mileage (fuel efficiency) than cars. A common belief is that because of this fact, a motorcycle might pay for itself. I wanted to believe this is true, but after running the numbers, this belief is a myth and is only true in extreme circumstances. I’m recording the relevant equations here so that next time I get the impulse to by a motorcycle, I won’t use cost savings as a justification.

In my situation, my everyday car, the Edscort, gets about 34 mpg highway, 30 mpg city. I don’t think I’ve ever seen less than 30 mpg so I’m going to use that figure as the Edscort’s fuel efficiency. The motorcycles in which I’ve been interested have been around $1500 in cost and achieve about 60 mpg. For simplicity’s sake, I will ignore the cost of insurance, maintenance, and accessories.

The cost, c, to drive a vehicle m miles is given by:

where f is the fuel efficiency of the vehicle in mpg and r is the cost of gasoline in $/gal. The cost savings Δc is the difference in the cost of driving those miles with the motorcycle (bike) vs. the Edscort (car). A negative value for Δc corresponds to money saved.

In order for the motorcycle to pay for itself, the cost savings must be at least as much as the purchase price of said motorcycle, P. That is, -Δc = P, where the negative sign makes a negative cost differential equal to a positive purchase price. The number of miles that must be driven before the bike pays for itself is therefore:

In my case, where the Edscort gets 30 mpg, the motorcycle gets 60 mpg, gas is $3/gal (as of this writing, it’s $2.99/gal down the road) and the motorcycle purchase price is $1500, I would need to drive the motorcycle 30,000 miles to break even. And note, these trips on the motorcycle must be in place of rides in the Edscort, not in addition to my usual driving.

To point out how impractical this is, consider that I’m currently averaging about 10,000 miles per year driven. If I can substitute the motorcycle for 20% of those miles, I’ll put 2,000 miles on the bike per year and it will pay for itself in only 15 years. I could cut that to 6 years if I substitute the bike for 1/2 of my normal driving. Ideally, I’d want the bike to pay for itself in 2 or 3 years, but that’s obviously not going to happen.

New bikes are considerably more expensive and I’ve not considered other ownership costs in which case things get even worse. Of course, reducing the wear and tear on the Edscort might stave off a significant repair bill, but there’s no guarantee that’s the case. Nor is there a guarantee that the bike won’t need a major repair itself.

The bottom line is that cost savings cannot be used to justify the purchase of a motorcycle. The decision to buy one is not a practical decision. Face it.